Lecture 11 Double Integrals Over Non-Rectangular Domains

Text References: Course notes pp. 37-52 & Rogawski 14.8, 15.1-15.2

11.1 Recap

Last time, we worked with double integrals over rectangular domains.

Exercise 11.1 Find the volume \(V\) of the solid enclosed between the graph of \(f(x,y)=16-x^2-3y^2\) and the rectangle \(R=[0,3]\times [0,1]\).

Solution. The volume of the solid is given by the double integral of \(f(x,y)\), which we can write as the following iterated integral: \[V=\displaystyle \iint_R (16-x^2-3y^2)dA = \int_0^3\int_0^1 (16-x^2-3y^2)dy dx\]

Evaluating the integral, we get \[\begin{align*} \int_0^3\int_0^1 (16-x^2-3y^2)dy dx & = \int_0^3 \left (16y-x^2y-y^3 \right|_{y=0}^1 dx \\ &= \int_0^3 15-x^2 dx \\ &= \left . 15x-\dfrac{1}{3}x^3\right|_{x=0}^3 \\ &= 36 \end{align*}\]

11.2 Learning Objectives

Given a region, classify it as Type I, Type II, or Type III.
Evaluate integrals over non-rectangular domains

11.3 Double Integrals Over Non-Rectangular Domains

Today, we’re going to work on integrating over types of regions which cannot be described as rectangles. We distinguish three types of region.

11.3.1 Type I Regions

A Type I region is one which can be described as lying between the graphs of two functions of \(x\) over some interval. That is, we have \(a\leq x\leq b\) and \(g(x)\leq y\leq h(x)\). In this case, we have \[\displaystyle \int_R f(x,y)dA = \int_a^b \int_{g(x)}^{h(x)}f(x,y) dy dx\]

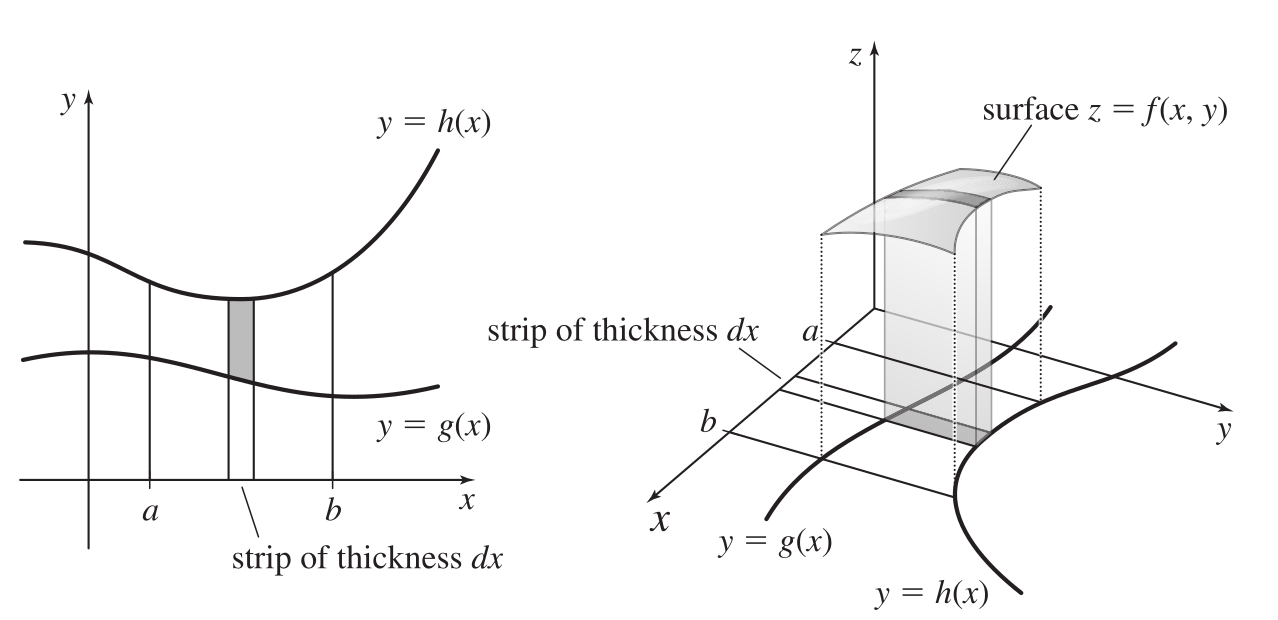
In the xy-plane, the area is bounded above by h(x), below by g(x), to the right by a and to the left by b. Taking a strip of thickness dx and projecting to the surface z=(x,y) gives a volume slice.

Figure 11.1: Type I regions

11.3.2 Type II Regions

A Type II region is one which can be described as lying between the graphs of two functions of \(y\) over some interval. That is, we have \(c\leq y\leq d\) and \(g(y)\leq x\leq h(y)\). In this case, we have \[\displaystyle \int_R f(x,y)dA = \int_c^d \int_{g(y)}^{h(y)}f(x,y) dx dy\]

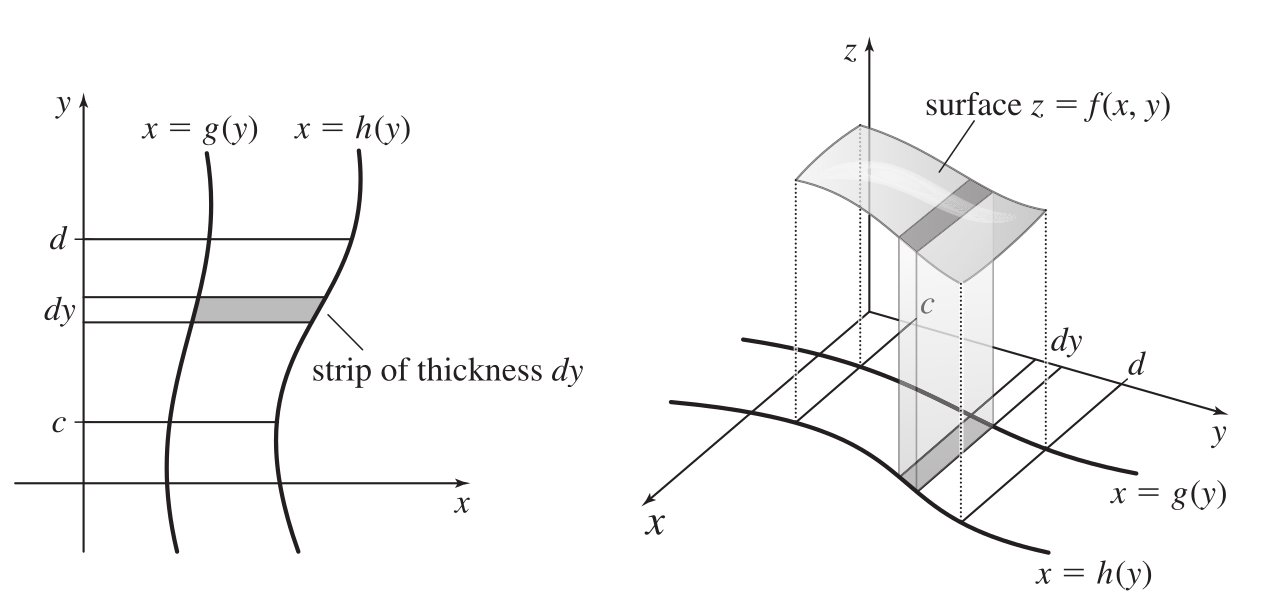
In the xy-plane, the area is bounded above by d, below by c, to the right by g(y) and to the left by h(y). Taking a strip of thickness dx and projecting to the surface z=(x,y) gives a volume slice.

Figure 11.2: Type II regions

11.3.3 Type III Regions

A Type III region is one that is neither Type I not Type II. Our approach in this case is to subdivide the region into smaller regions which are of one type or the other.

11.4 Exercises

A good strategy for solving problems involving integration over non-rectangular domains is to start by sketching the region, identifying its type, and then setting up and solving the integral.

Exercise 11.2 Evaluate \(\displaystyle \iint_R xy dA\) where \(R\) is the triangular region with vertices \((0,0)\), \((2,0)\), and \((0,1)\).

Solution. Let’s start by sketching the region. Note that we can set this up either as a Type I or Type II region.

Let’s classify it as Type I to start:

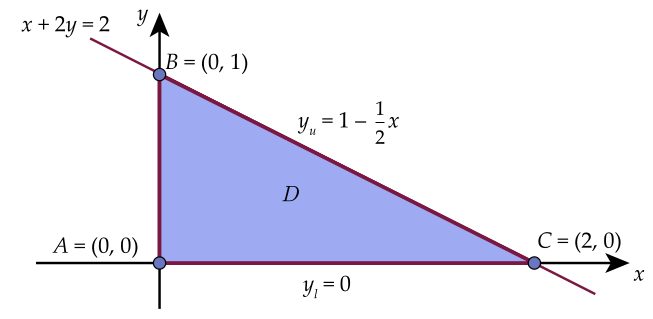
Triangle with vertices (0,0), (2,0), and (0,1) in the xy plane. The triangle is bounded below by y=0 and above by y=1-1/2x while x ranges from 0 to 2.

Figure 11.3: Sketch of \(R\)

The region \(R\) can be described by \[0\leq x \leq 2 \quad \mbox{and}\quad 0\leq y\leq 1-\dfrac{1}{2}x\]

Writing the integral, we get

\[\begin{align*} \displaystyle \iint_R xy dA & = \int_0^2\int_0^{1-\frac{1}{2}x}xy dy dx \\ &= \int_0^2 x\left (\dfrac{y^2}{2}\right |_{y=0}^{1-\frac{1}{2}x} dx\\ &= \dfrac{1}{2}\int_0^2 x\left (1-\dfrac{1}{2}x \right)^2 dx\\ &= \left ( \dfrac{x^2}{4}-\dfrac{1}{6}x^3+\dfrac{1}{32}x^4 \right|_{0}^2\\ &=\dfrac{1}{6} \end{align*}\]

If, instead, we set this up as a Type II integral, we might change our sketch as follows:

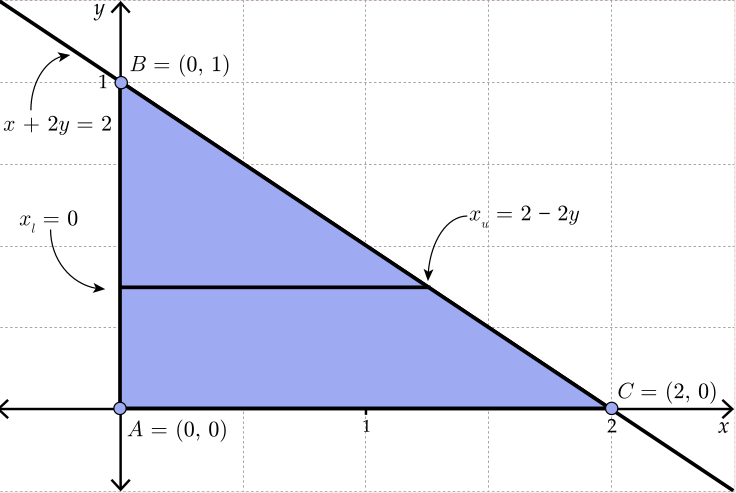
Triangle with vertices (0,0), (2,0), and (0,1) in the xy plane. The triangle is bounded on the left by x=0 and on the right by x=2-2y while y ranges from 0 to 1.

Figure 11.4: Sketch of \(R\)

The region \(R\) can be described by \[0\leq y\leq 1 \quad \mbox{and}\quad 0\leq x \leq 2-2y\]

Writing the integral, we get

\[\begin{align*} \displaystyle \iint_R xy dA & = \int_0^1\int_0^{2-2y}xy dx dy \\ &= \int_0^1 y \left (\dfrac{x^2}{2}\right |_{x=0}^{2-2y} dy\\ &= 2\int_0^1 y(1-y)^2 dy\\ &=\dfrac{1}{6} \end{align*}\]

Exercise 11.3 Evaluate \(\displaystyle \int_0^1\int_0^y e^{x^2}dxdy\).

Solution. Note that integrating first with respect to \(x\) is not to our advantage; we can change the order of integration (and also the bounds!) to simplify things.

The region is the triangle with vertices \((0,0)\), \((1,0)\), and \((1,1)\):

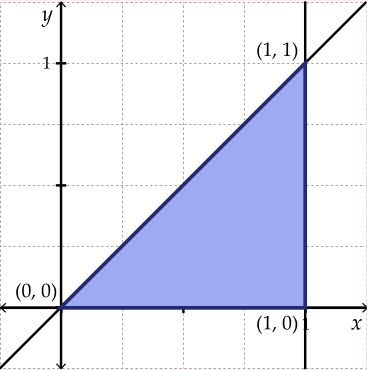
Triangle with vertices (0,0), (1,0), and (1,1) in the xy plane. The triangle is bounded above by y=x and below by y=0 while x ranges from 0 to 1.

Figure 11.5: Sketch of \(R\)

The region \(R\) can be described by \[0\leq x\leq 1 \quad \mbox{and}\quad 0\leq y \leq x\]

Writing the integral, we get

\[\begin{align*} \displaystyle \iint_R e^{x^2} dA & = \int_0^1\int_0^{x}e^{x^2} dy dx \\ &= \int_0^1 y \left . e^{x^2}\right |_{y=0}^{x} dx\\ &= \int_0^1 xe^{x^2} dx\\ &=\dfrac{e-1}{2} \end{align*}\]

Exercise 11.4 Find the volume \(V\) of the region under the plane \(z=2x+3y\) and above the triangle shown in the figure below

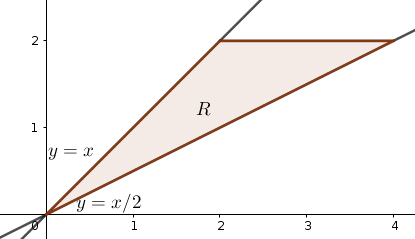
Triangle with vertices (0,0), (2,2), and (4,2) in the xy plane. The triangle is bounded above by x=y and below by x=2y while y ranges from 0 to 2.

Figure 11.6: Sketch of \(R\)

Solution. The simplest way to set up is integral is using a Type II region. Describing it as Type I is possible, but would require setting up two integrals instead of one (why?).

The region \(R\) can be described by \[0\leq y\leq 1 \quad \mbox{and}\quad y\leq x \leq 2y\]

Writing the integral, we get

\[\begin{align*} \displaystyle \iint_R 2x+3y dA & = \int_0^2\int_y^{2y}2x+3y \, dx dy \\ &= \int_0^2 \left (x^2+3yx \right |_{x=y}^{2y} dy\\ &= \int_0^2 6y^2 dy \\ &= 16 \end{align*}\]