Lecture 15 Triple Integrals

Text References: Course notes pp. 66-74 & Rogawski 15.3-15.6

15.1 Recap

Last time, we discussed various interpretations of double integrals (which can be generalized to triple integrals).

Exercise 15.1 Find the average value of \(f(x,y)=xy^2\) on the box \([0,1]\times[0,2]\).

Solution. The average value is given by \(\displaystyle f_{avg}=\frac{1}{\mbox{Area}(R)}=\iint_R f(x,y)dA\).

Here, \(R)= [0,1]\times[0,2]\) which has area \(2\).

\[\begin{align*} f_{avg}=\frac{1}{\mbox{Area}(R)}=\iint_R f(x,y)dA&=\frac{1}{2} \int_0^1 \int_0^2 xy^2 dy dx\\ &= \frac{1}{2} \left .\int_0^2 x \frac{y^3}{3} \right |_{y=0}^2 dx\\ &= \frac{1}{2} \int_0^2 \frac{8x}{3} dx \\ &= \frac{4}{3} \end{align*}\]

15.2 Learning Objectives

• Evaluate triple integrals by generalizing techniques for solving double integrals.

15.3 Triple Integrals

The intuition for triple integrals is similar to that for double integrals. This time, our domains of integration are 3D regions of space rather than 2D regions. Partitioning the domain into small cubes is done by partitioning the \(x\), \(y\), and \(z\) axes into intervals of length \(\Delta x\), \(\Delta y\), and \(\Delta z\). In each cube, we pick a point \((x_i^*, y_j^*, z_k^*)\), evaluate the function \(f(x,y,z)\) at that point, and multiply the result by the volume of the box \(\Delta V = \Delta x\Delta y\Delta z\). Summing the results for each cube in the domain and taking the limit as \(\Delta x\), \(\Delta y\), and \(\Delta z\) go to zero, we get the triple integral \(\displaystyle \iiint_D f(x,y,z) dV\).

As you might expect, many of the techniques that we developed to solve double integrals also apply to triple integrals.

15.3.1 Triple Integrals over Rectangles

Suppose that the domain of integration \(D\) is a rectangular box with \(x\in[a_1,a_2]\), \(y\in[b_1,b_2]\), and \(z\in[c_1,c_2]\). As in the case of double integrals, we can change the orders of integration, of which there are now six instead of two.

Exercise 15.2 Evaluate \(\displaystyle \iiint_D x^2+y^2+z^2 dV\) where \(D\) is the box \([0,1]\times [0,2] \times [0,3]\).

Solution. The box can be described buy the inequalities \(0\leq x \leq 1\), \(0\leq y \leq 2\), and \(0\leq z \leq 3\). We have

\[\begin{align*} \iiint_D x^2+y^2+z^2 dV &= \int_0^1 \int_0^2\int_0^3 (x^2+y^2+z^2)~dz dy dx \\ &= \int_0^1 \int_0^2 \left. x^2 +y^2 + \frac{z^3}{3}\right |_{z=0}^3 ~dy dx \\ &= \int_0^1 \int_0^2 (3x^2+3y^2+9)~ dy dx \\ &= \int_0^1 6x^2+26 \\ &= 28 \end{align*}\]

15.3.1.1 Triple Integrals over Non-Rectangular Regions

For non-rectangular regions, we can extend the concept of Type I, Type II, and Type III regions and find at least seven types. At this point, we don’t bother numbering them, but the principles remain the same.

The analogue to Type I in three dimensions is a domain which can be described as \(D=\{(x,y,z)\mid a\leq x\leq b, \phi_1(x)\leq y\leq \phi_2(x), \gamma_1(x,y) \leq z \leq \gamma_2(x,y)\}\). Note how \(x\) is bounded by constants, \(y\) is bounded by functions of \(x\), and \(z\) is bounded by functions of \(x\) and \(y\). The corresponding integral is \[\iiint_D f(x,y,z) = \int_a^b \int_{\phi_1(x)}^{\phi_2(x)}\int_{\gamma_1(x,y)}^{\gamma_2(x,y)}f(x,y,z)~dzdydx\]

Note that setting up the integral this way ensure that we get a number. This is a definite integral, so we expect a numerical value as output. Working our way inwards, for the values of \(x\) between \(a\) and \(b\), the values of \(y\) range from \(\phi_1(x)\) to \(\phi_2(x)\) (remember, this is how things worked for double integrals). Then, for each point in the two-dimensional region just described, the values of \(z\) range from \(\gamma_1(x,y)\) to \(\gamma_2(x,y)\).

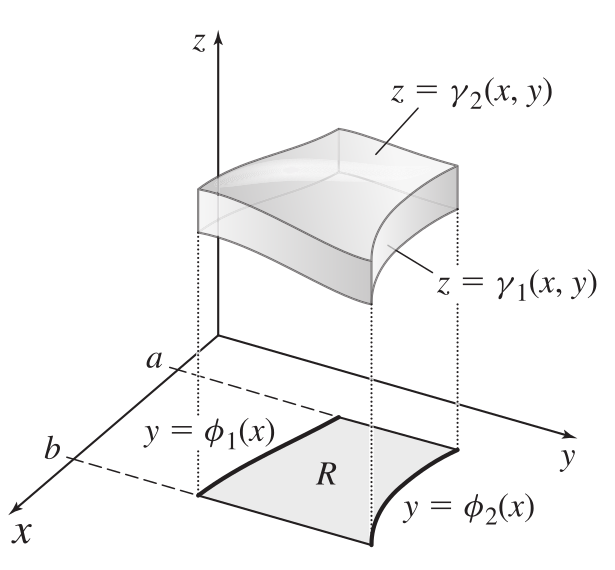
Figure 15.1: Type I triple integral

Exercise 15.3 Evaluate \(\displaystyle \iiint_D y~dV\) where \(D\) is the prism bounded by the planes \(x=0, x=2, y=0, z=0,\), and \(y+z=1\).

Solution. The prism can be described by the inequalities \(0\leq x\leq 2\), \(0\leq y \leq 1\), and \(0\leq z\leq 1-y\). We can set up and solve the following integral:

\[\begin{align*} \iiint_D y~dV &= \int_0^2\int_0^1\int_0^{1-y}~dzdydx \\ &= \int_0^2 \int_0^1 1-y^2~dydx\\ &= \int_0^2 \frac{1}{6}~dx\\ &= \frac{1}{3} \end{align*}\]

Exercise 15.4 Evaluate \(\displaystyle \iiint_D \frac{z}{4-y} dV\) where \(D\) is the region lying in the first octant bounded by the cylinder \(y^2+z^2=4\) and the planes \(x+y=2\), \(x+2y=6\), \(z=0\), and \(y=0\).

Solution. Note that we can describe \(x\) in terms of \(y\) using the inequalities \(2-y\leq x\leq 6-2y\) and we can describe \(z\) using the inequalities \(0\leq z\leq \sqrt{4-y^2}\). The value of \(y\) is restricted to be between \(0\) (condition \(y=0\)) and \(2\) (condition \(\sqrt{4-y^2}\)).

Given that \(y\) is bounded by constants, we will integrate last with respect to \(y\); the other two conditions are interchangeable. However, things will be simpler if we integrate first with respect to \(x\) since the integrand is not a function of \(x\).

We have

\[\begin{align*} \iiint_D \frac{z}{4-y} dV & = \int_0^2 \int_{0}^{\sqrt{4-y^2}}\int_{2-y}^{6-2y} \frac{z}{4-y}~dxdzdy \\ &= \int_0^2 \int_{0}^{\sqrt{4-y^2}} z~dz dy\\ &= \int_0^2 \frac{4-y^2}{2}~dy\\ &= \frac{8}{3} \end{align*}\]