Lecture 7 Gradients and Directional Derivatives

Text References: Course notes pp. 26-37 & Rogawski 14.5-14.7

7.1 Recap

Last time, we learned how to use dependence trees to compute Chain Rules.

Exercise 7.1 Let \(z=f(x,y)\) where \(x=r\cos(\theta)\) and \(y=r\sin(\theta)\). If \(z=x^2y\), use the Chain Rule to calculate \(\left. \dfrac{\partial z}{\partial r} \right|_{r=1,\theta=0}\)

Solution. The dependence tree is as follows:

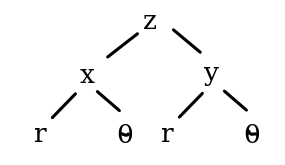
Figure 7.1: Dependence tree of \(z=f(x,y)\) where \(x=g(r,\theta)\), and \(y=h(r,\theta)\)

To calculate the partial derivative of \(z\) with respect to \(r\), we must follow and sum the paths that start from \(z\) and end at \(r\). We get \[\dfrac{\partial z}{\partial r} = \dfrac{\partial z}{\partial x}\dfrac{\partial x}{\partial r}+ \dfrac{\partial z}{\partial y}\dfrac{\partial y}{\partial r}\]

We have

• \(\dfrac{\partial z}{\partial x} = 2x\)
• \(\dfrac{\partial z}{\partial y} = x^2\)
• \(\dfrac{\partial x}{\partial r} = \cos(\theta)\)
• \(\dfrac{\partial y}{\partial r} = \sin(\theta)\)

At \((r,\theta)=(1,0)\), we have \(x(1,0)=1\) and \(y=(1,0)=0\). Substituting everything into the Chain Rule, we get \[\left .\dfrac{\partial z}{\partial r}\right|_{r=1, \theta=0} =2(1)(1)+ 1^2(0)=2\]

7.2 Learning Objectives

• Given a function of several variables, calculate its gradient vector and evaluate it at a point.
• Given a function of several variables and a point, calculate its directional derivative in the direction of a vector.

7.3 The Gradient Vector

We define the gradient vector of \(f(x,y)\) as \[\nabla f = \left(\dfrac{\partial f}{\partial x},\dfrac{\partial f}{\partial y}\right)\]

The gradient vector is very useful for making a lot of notation more compact:

• The linear approximation \(f(x,y)\approx f(a,b)+f_x(a,b)(x-a)+f_y(a,b)(y-b)\) can be written using the gradient as \(f(\vec{r})=f(\vec{a})+\nabla f(\vec{a})\cdot(\vec{r}-\vec{a})\)
• The basic chain rule \(\dfrac{dz}{dt}=\dfrac{\partial f}{\partial x}\dfrac{dx}{dt}+\dfrac{\partial f}{\partial y}\dfrac{dy}{dt}\) can be written as \(\nabla f (\vec{r}(t))\cdot \vec{r}'(t)\)

7.4 Directional Derivatives

With partial derivatives, we’ve seen how to determine the rate of change of a multivariate function as we move in the positive \(x\) and positive \(y\) directions. What if we want to determine the rate of change in some other direction? The directional derivative will help us here.

Definition 7.1 The directional derivative of \(f(x,y)\) in the direction of a unit vector \(\vec{u}=(u_1, u_2)\) at the point \(\vec{a}=(a,b)\) is denoted by \(D_{\vec{u}}f(a,b)\) and defined as \[D_{\vec{u}}f(a,b=\displaystyle \lim_{h\to 0}\dfrac{f(\vec{a}+h\vec{u})-f(\vec{a})}{h}=\lim _{h\to 0}\dfrac{f(a+hu_1, b+hu_2)-f(a,b)}{h}\]

Note that since \(a,b,u_1, and u_2\) are constants, the expression \(f(a+hu_1, b+hu_2)\) is really just a function of \(h\)–let’s call it \(g(h)=f(a+hu_1, b+hu_2)\). Not only that, but the directional derivative \(D_{\vec{u}}f(a,b)\) is none other than the derivative of \(g\) function at \(h=0\).

We have \(g(h)=f(x(h), y(h)\) where \(x(h)=a+hu_1\) and \(y(h)=b+hu_2\). Applying the Chain Rule, we have \[\begin{align*} g'(h) &= \dfrac{\partial f}{\partial x}\dfrac{dx}{dh}+\dfrac{\partial f}{\partial y}\dfrac{dy}{dh}\\ &= \dfrac{\partial f}{\partial x}u_1 + \dfrac{\partial f}{\partial y} u_2\\ &= \nabla f(x,y)\cdot\vec{u} \end{align*}\] When \(h=0\), we have \(g'(0)=\nabla f(a,b)\cdot\vec{u}\) and therefore \[D_{\vec{u}}f(a,b) = \nabla f(a,b)\cdot\vec{u}\] which is a much more compact way of expressing and calculating directional derivatives!

Exercise 7.2 Find the directional derivative of \(f(x,y)=2x^3+4xy^2+y\) at the point \((-1,1)\) in the direction of the vector \((1,1)\).

Solution. First, we note that the vector \((1,1)\) is not a unit vector, so we must normalize it. We get \[\vec{u}=\dfrac{1}{\Vert (1,1)\Vert}(1,1)=\dfrac{1}{\sqrt{2}}(1,1)\] Then, \[\nabla f(x,y) = (6x^2+4y^2, 8xy+1) \quad \mbox{so} \quad \nabla f (-1,1)=(10,-7)\] Therefore, \[D_{\vec{u}}f(-1,1)=\nabla f(-1,1)\cdot\left (\dfrac{1}{\sqrt{2}}, \dfrac{1}{\sqrt{2}}\right ) = \dfrac{3}{\sqrt{2}}\]

7.5 The Gradient Vector and Directional Derivatives

Given that there are infinitely many directional derivatives of a function \(f(x,y)\) at a point \((a,b)\), it’s natural to wonder in which direction the directional derivative assumes its largest value. In other words, in which direction is the greatest rate of change?

Thinking back to the dot product for a moment, recall that \(\vec{a}\cdot\vec{b}=\Vert\vec{a}\Vert| \Vert\vec{b}\Vert\cos(\theta)\), where \(\theta\) is the angle between \(\vec{a}\) and \(\vec{b}\). Applying this idea to the formula for the directional derivative, we find that \[\begin{align*} D_{\vec{u}}f(a,b)&=\nabla f(a,b)\cdot \vec{u} \\ &= \Vert \nabla f(a,b)\Vert \Vert \vec{u} \Vert \cos(\theta)\\ &= \Vert \nabla f(a,b)\Vert \cos(\theta) \quad \mbox{since $\vec{u}$ is a unit vector} \end{align*}\] Thus, \(D_{\vec{u}}f(a,b)\) assumes its largest value when \(\theta=0\), i.e., when \(\vec{u}\) is in the direction of \(\nabla f(a,b)\). The maximum value is given by \(\Vert \nabla f(a,b)\Vert\).

So, at any given point, the gradient vector gives the direction and the magnitude of the steepest slope of the graph of \(f\).

Exercise 7.3 Find the largest rate of change of \(f(x,y)=2x^3+4xy^2+y\) at the point \((-1,1)\) and the direction in which it occurs.

Solution. We found previously that \[\nabla f(x,y) = (6x^2+4y^2, 8xy+1)\] The largest rate of change of \(f\) at \((-1,1)\) is \[\Vert \nabla f(-1,1)\Vert = \Vert (10,7)\Vert = \sqrt{10^2+7^2} = \sqrt{149}\] and occurs in the direction \(\vec{u}=\nabla f(-1,1)=(10,7)\)

To get a geometric intuition for what’s happening, take a look at this interactive applet. Use the slider for \(k\) to move onto a different level curve of the function. Click and drag the point \(A\) and observe how its gradient changes. What do you notice about the direction of the gradient and the level curves?