Lecture 6 Chain rule for paths

Text References: Course notes pp. 26-37 & Rogawski 14.5-14.7

6.1 Recap

Last time, we learned how to parametrize several different types of curves and to represent these parametrizations using vector functions.

Exercise 6.1 What does the path of the particle described by \(x(t)=\cos(t), y(t)=\sin(t), z(t)=-t\) for \(0\leq t \leq 10\) look like?

1. a circle in the \(xz\)-plane
2. a helix on which the particle is travelling up
3. a helix on which the particle is travelling down
4. a sine wave in the \(xz\)-plane

Solution. Recall that on the \(xy\)-plane, \(x(t)=\cos(t), y(t)=\sin(t)\) parametrizes a circle. Thus, viewed from above, the particle is travelling on the unit circle. This means that the particle is following a helical path. As the value of \(t\) increases, the value of \(z\) decreases and therefore the particle is travelling downward.

See what’s happening in 3D space

6.2 Learning Objectives

• Apply the Chain Rule to calculate derivatives of multivariate functions with arbitrarily many intermediate and independent variables

6.3 Chain Rule for Paths

Consider a function \(f(x,y)\) where \(x\) and \(y\) are themselves functions of a parameter \(t\). Setting \(z=f(x,y)\), we can represent the relationship between the variables with a dependence tree: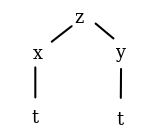

Figure 6.1: Dependence tree of \(z=f(x,y)\) where \(x\) and \(y\) are both functions of \(t\)

This dependence tree is useful in Chain Rule calculations. Given \(z=f(x,y)\) where \(x\) and \(y\) are themselves functions of a parameter \(t\), we realize that \(z\) does, in fact, depend on the parameter \(t\) (via \(x(t)\) and \(y(t)\). One question we can ask ourselves is how to determine the derivative of \(z\) with respect to \(t\). From our differentials, we get \[dz=\dfrac{\partial z}{\partial x}dx + \dfrac{\partial z}{\partial y}dy\] dividing by the infinitesimal \(dt\), we get the Chain Rule for Paths: \[\dfrac{dz}{dt}=\dfrac{\partial z}{\partial x}\dfrac{dx}{dt}+\dfrac{\partial z}{\partial y}\dfrac{dy}{dt}\]

Notice how there is one summand for each path in the dependence tree, and that each summand is gotten by multiplying the appropriate derivatives, which we can find by looking at the branches!

Exercise 6.2 Let \(z=f(x,y)=1+x^2+y^2\) with \(x(t)=e^t\sin(t)\) and \(y(t)=2e^t\cos(t)\). Find the value of \(\dfrac{dz}{dt}\) at \(t=0\).

Solution. By the Chain Rule for paths, we know that \(\dfrac{dz}{dt}=\dfrac{\partial z}{\partial x}\dfrac{dx}{dt}+\dfrac{\partial z}{\partial y}\dfrac{dy}{dt}\). Let’s break things into smaller pieces.

• \(\dfrac{\partial z}{\partial x}=2x\)
• \(\dfrac{\partial z}{\partial y}=2y\)
• \(\dfrac{dx}{dt}=e^t\sin(t)+e^t\cos(t)\)
• \(\dfrac{dy}{dt}=2e^t\cos(t)-2e^t\sin(t)\)

Putting things together, we get \[\dfrac{dz}{dt}= 2x (e^t\sin(t)+e^t\cos(t)) + 2y(2e^t\cos(t)-2e^t\sin(t))\]

Now, we can use the fact that \(t=0\), substitute it in the above equation, and use it to find \(x(0)=0\) and \(y(0)=2\) to get \[\left .\dfrac{dz}{dt}\right|_{t=0} = 2(0)(0+1)+2(2)(2-0)=8\]

6.4 Generalized Chain Rule

Now, let’s consider \(z=f(x,y)\) where \(x\) and \(y\) are themselves multivariate functions. Let’s suppose that \(x=g_1(s,t)\) and \(y=g_2(s,t)\). We have the following dependence tree: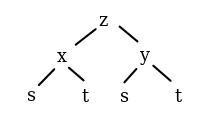

Figure 6.2: Dependence tree of \(z=f(x,y)\) where \(x=g_1(s,t)\) and \(y=g_2(s,t)\)

Now, \(z\) depends on both \(s\) and \(t\). Using the tree as a guide, we can calculate the partial derivatives of \(z\) with respect to these two variables: \[\begin{align*} \dfrac{\partial z}{\partial s}& = \dfrac{\partial z}{\partial x}\dfrac{\partial x}{\partial s} +\dfrac{\partial z}{\partial y}\dfrac{\partial y}{\partial s} \\ \dfrac{\partial z}{\partial t} &=\dfrac{\partial z}{\partial x}\dfrac{\partial x}{\partial t} +\dfrac{\partial z}{\partial y}\dfrac{\partial y}{\partial t} \end{align*}\]

Let’s pay attention to notation for a moment:

• We use \(\partial\) to denote a partial derivative; that is, when the function being differentiated depends on more than one variable
• We use \(d\) to denote a derivative; that is, when the function being differentiated depends on a single variable.

Exercise 6.3 Let \(z=f(x,y)\) where \(x=g(r,s)\), \(y= h(r)\), and \(r=p(t)\). Draw the dependence diagram and give the Chain Rule for \(\dfrac{\partial z}{\partial s}\) and \(\dfrac{\partial z}{\partial t}\)

Solution. The dependence tree is as follows:

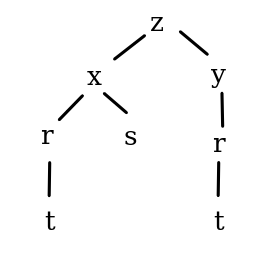
Figure 6.3: Dependence tree of \(z=f(x,y)\) where \(x=g(s,t)\), \(y=h(r)\), and \(r=p(t)\)

To calculate the partial derivative of \(z\) with respect to \(s\), we must follow and sum the paths that start from \(z\) and end at \(s\). We get \[\dfrac{\partial z}{\partial s} = \dfrac{\partial z}{\partial x}\dfrac{\partial x}{\partial s}\]

To calculate the partial derivative of \(z\) with respect to \(t\), we must follow and sum the paths that start from \(z\) and end at \(t\). We get \[\dfrac{\partial z}{\partial t} = \dfrac{\partial z}{\partial x}\dfrac{\partial x}{\partial r}\dfrac{dr}{dt}+\dfrac{\partial z}{\partial y}\dfrac{\partial y}{\partial r}\dfrac{dr}{dt}\]