Lecture 18 Newton’s Method
Text References: Course notes pp. 75-100 & Rogawski 4.8, 10.7
18.1 Recap
Last time, we discussed changing variables to spherical coordinates.
Exercise 18.1 Which of the following integrals give the volume of the unit sphere?
- \(\displaystyle \int_{0}^{2\pi} \int_0^{2\pi}\int_{0}^{1} ~drd\phi d\theta\)
- \(\displaystyle \int_{0}^{\pi} \int_0^{2\pi}\int_{0}^{1} ~drd\phi d\theta\)
- \(\displaystyle \int_{0}^{\pi} \int_0^{2\pi}\int_{0}^{1} r^2\sin(\theta)~drd\phi d\theta\)
- \(\displaystyle \int_{0}^{\pi} \int_0^{2\pi}\int_{0}^{1} r^2\sin(\theta)~drd\theta d\phi\)
- \(\displaystyle \int_{0}^{\pi} \int_0^{2\pi}\int_{0}^{1} r~drd\theta d\phi\)
Solution. The answer is c. We must remember the Jacobian, which is equal to \(r^2\sin(\theta)\) and match the bounds: \(0\leq \theta \leq \pi\) and \(0\leq \phi \leq 2\pi\).
18.2 Learning Objectives
- Use Newton’s Method to find roots of polynomial equations.
18.3 Finding Roots of Polynomials
We’re now going to switch back to working with functions of one variable. One type of problem that we’d like to solve is that of finding the roots of an equation, i.e. solving \(f(x)=0\)interpola=1-x. solt . We’re used to solving these problems algebraically, but this isn’t always possible. Instead, we’re going to develop numerical methods which can give us a good approximation of the roots.
As an example, consider the equation \(x^5=1-x\). If we want to find its solutions, we are solving \(x^5+x-1=0\); however there isn’t a nice way of doing this algebraically.
Looking at the graph of this function, we notice that the root is located somewhere between \(x=0.5\) and \(x=1\).
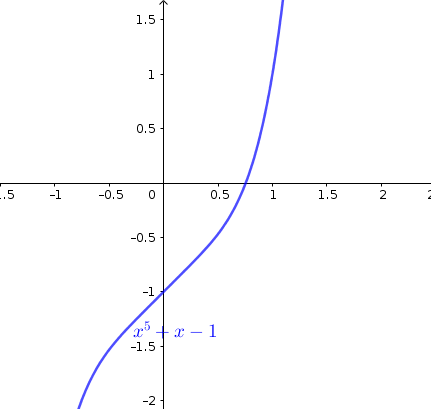
Figure 18.1: Graph of \(x^5+x-1\)
So, instead of finding exact solutions or roots to equations, we will have to make do with approximating roots or solutions.
18.4 Newton’s Method
Newton’s Method is an iterative method for approximating roots of a function \(f(x)=0\), consisting of two main steps:
- Step 1: Choose an initial guess \(x_0\) that is close to the desired root, if possible.
- Step 2: Generate successive approximations \(x_2, x_2\ldots\) where \(x_{n+1}=x_n-\dfrac{f(x)n}{f'(x_n)}\)
We can derive the formula in Step 2 by thinking about the linear approximation of \(f(x)\) at the point \(x_0\), which is given by \(L_{x_0}(x)=f(x_0)+f'(x_0)(x-x_0)\). This is the tangent line at \(x_0, f(x_0)\), which will cross the \(x\)-axis at the point \((x_1,0)\). Plugging this into the equation for the linear approximation and solving for \(x_1\), we get \[0=f(x_0)+f'(x_0)(x_1-x_0) \implies x_1=x_0+\dfrac{f(x_0)}{f'(x_0)}\] The same reasoning applies for \(x_2\) and so on.
In this interactive applet we have an example of how Newton’s Method works on the function \(f(x)=\frac{x^2}{2}+x+1-e^x\).
As with any numerical method, there are some caveats to keep in mind when using Newton’s Method:
- The method will not converge if:
- \(f'(x)\) does not exist or is not continuous at the root
- \(f'(x)=0\) at the root
- \(f''(x)\) is infinite at the root
- The method will converge rapidly as long as the initial guess for \(x_0\) is good enough. A poor guess might result convergence to a different root or divergence. Coming up with a reasonable guess can be done by looking at the graph of the function.
- In practice, it is usually safe to assume that if \(x_n\) and \(x_{n+1}\) agree to \(m\) decimal places, then the approximation is correct to these \(m\) places.
Exercise 18.2 Find a root of the function \(f(x)=x^5+x-1\), correct to five decimal places.
Solution. We have \(f'(x)=5x^4+1\). Looking at the graph of the function, we can set \(x_0=1\) as our initial guess for the root. Then,
\[\begin{align*} x_1 &=x_0-\dfrac{f(x_0)}{f'(x_0)}=1-\dfrac{1}{6}=\frac{5}{6}\approx 0.83333 \\ x_2 &= x_1-\dfrac{f(x_1)}{f'(x_1)}\approx 0.76438 \\ x_3 &= x_2-\dfrac{f(x_2)}{f'(x_2)}\approx 0.75502 \\ x_4 &= x_3-\dfrac{f(x_3)}{f'(x_3)}\approx 0.75488 \\ x_5 &= x_4-\dfrac{f(x_4)}{f'(x_4)}\approx 0.75488 \\ \end{align*}\]
Note that at this point, the first five decimal places are no longer changing; this is the root, to five decimal places of accuracy.
Exercise 18.3 Use three iterations of Newton’s Method to find the smallest positive solution to \(\sin(3x)=\cos(x)\).
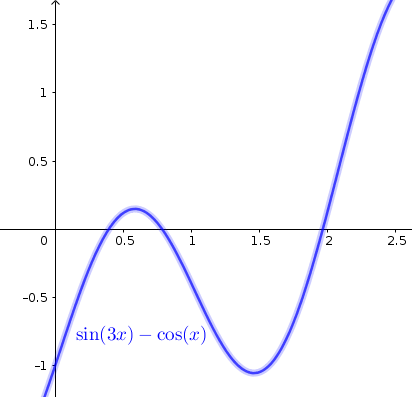
Figure 18.2: Graph of \(\sin(3x)-\cos(x)\)
Solution. A solution to \(\sin(3x)=\cos(x)\) is a root of \(f(x)=\sin(3x)-\cos(x)=0\). Looking at the graph of the function, we notice that the smallest root is located between \(x=0\) and \(x=0.5\). Let’s use \(x_0=0.5\) as our initial guess.
We have \(f'(x)=3 \cos(3x)+\sin(x)\), which gives the formula \[x_{n+1}=x_n+\frac{\sin(3x_n)-\cos(x_n)}{ \cos(3x_n)+\sin(x_n)}\] With \(x_0=0.5\) as the first guess, we have
\[\begin{align*} x_1 \approx 0.326625\\ x_2 \approx 0.385204\\ x_3 \approx 0.392569 \end{align*}\]