Lecture 16 Cylindrical Coordinates

Text References: Course notes pp. 66-74 & Rogawski 15.3-15.6

16.1 Recap

Last time, we generalized our results and techniques for solving double integrals in order to solve triple integrals.

Exercise 16.1 Which of the following integrals is equal to \(\displaystyle \int_0^3 \int_0^2\int_0^y f(x,y,z)~dzdydx\)?

1. \(\displaystyle \int_0^2 \int_0^3\int_0^y f(x,y,z)~dzdxdy\)
2. \(\displaystyle \int_0^2 \int_0^3\int_0^y f(x,y,z)~dzdydx\)
3. \(\displaystyle \int_0^3 \int_0^2\int_0^y f(x,y,z)~dxdydz\)
4. \(\displaystyle \int_0^3 \int_0^2\int_0^z f(x,y,z)~dydzdx\)

You can use this interactive applet to view the region in 3D.

Solution. The region can be described by the inequalities \(0\leq x\leq3\), \(0\leq y \leq 2\), and \(0\leq z\leq y\). Option a is simply swapping the constant bounds so it is equal to the initial integral.

16.2 Learning Objectives

• Evaluate triple integrals by using an appropriate change to cylindrical coordinates.

16.3 Cylindrical Coordinates

So far, we’ve generalized most of our integration techniques from double to triple integrals. The last thing we’ll cover on this topic are two key changes of variable: cylindrical coordinates and spherical coordinates.

Cylindrical coordinates are the 3D analogue to polar coordinates. In fact, the transformation is quite similar: \[x=\rho\cos(\phi), \quad y=\rho\sin(\phi), \quad\mbox{and}\quad z=z\]

Note that \(0\leq\phi < 2\pi\).

This interactive applet might give you a geometric intuition for this coordinate system.

The Jacobian of this change of variables is \[\frac{\partial (x,y,z)}{\partial (\rho,\phi, z)}=\det \begin{bmatrix}x_{\rho}& x_{\phi}& x_{z} \\ y_{\rho}& y_{\phi}& y_{z} \\ z_{\rho}& z_{\phi}& z_{z} \end{bmatrix}=\det \begin{bmatrix}cos(\phi)& -\rho\sin(\phi) & 0 \\ \sin(\phi) & \rho\cos(\phi) & 0 \\ 0 & 0 & 1\end{bmatrix}=\rho\]

So, when changing from Cartesian to cylindrical coordinates, we can replace \(dzdydx\) with \(\rho~dzd\rho d\phi\), and this will almost always be the desired order of differentials.

Exercise 16.2 A wedge is cut from the cylinder \(x^2+y^2=4\) , by the planes \(z=0\) and \(z=3y\) , where \(y\) is assumed to be non-negative. Find the volume of the wedge.

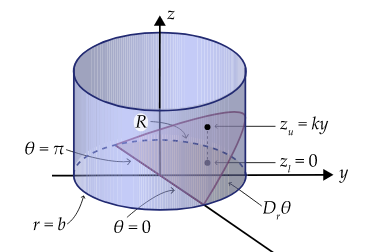
Figure 16.1: Sketch of the wedge

Solution. Converting the cylinder and the planes to cylindrical coordinates, we get \[x^2+y^2=4 \to \rho=2, \quad z=0 \to z=0, \quad z=3y\to z=3\rho\sin(\phi) \]

We can therefore describe the wedge using the following inequalities: \[0\leq \rho\leq 2, \quad 0\leq \phi\leq \pi,\quad \mbox{and}\quad 0\leq z \leq 3\rho\sin(\phi)\]

The last piece we need to recall is that the volume is given by \(\displaystyle V=\iiint_R 1~dV\).

Applying the change of variables, we get

\[\begin{align*} V & =\iiint_R 1~dV\\ &= \int_0^{\pi}\int_0^2\int_0^{3\rho\sin (\phi)} \rho~dzd\rho d\phi\\ &= \int_0^{\pi}\int_0^2 3\rho^2\sin(\phi)~d\rho d\phi\\ &= \int_0^{\pi} 8\sin(\phi)~d\phi \\ &= 16 \end{align*}\]