Lecture 12 Double Integrals in Polar Coordinates

Text References: Course notes pp. 53-65 & Rogawski 11.3, 15.4-15.6

12.1 Recap

Last time, we worked with double integrals over non-rectangular domains.

Exercise 12.1 Use inequalities to describe the region pictured below:

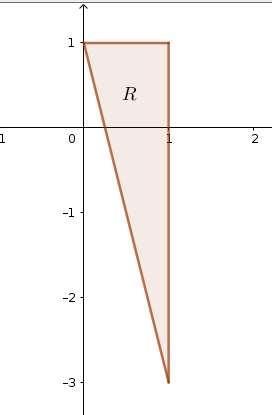
Figure 12.1: Triangle in the \(xy\)-plane

Solution. The region \(R\) can be described by \[-3\leq y \leq 1 \quad \mbox{and}\quad \dfrac{1-y}{4}\leq x\leq 1\] or by \[0\leq x\leq 1 \quad \mbox{and}\quad -4x+1\leq y \leq 0 \]

12.2 Learning Objectives

• Evaluate integrals using polar coordinates.

12.3 Polar Coordinates

The techniques that we’ve seen so far for setting up and evaluating double integrals are not always suited for more complicated regions. We’re going to start building up a key tool in our integration toolkit, starting with a discussion of polar coordinates.

Polar coordinates are particularly useful when the domain \(R\):

• is circular or has circles forming part of its boundary; and
• contains the expression \(x^2+y^2\) (which will become \(\rho^2\) after changing to polar coordinates)

Recall that to convert from Cartesian coordinates to polar coordinates, we set \(x= \rho \cos(\phi)\) and \(y=\rho\sin(\phi)\).

12.4 Double Integrals in Polar Coordinates

The question now becomes how to transform our original integral \(\displaystyle \iint_R f(x,y)dA\) to polar coordinates. We can substitute \(x= \rho \cos(\phi)\) and \(y=\rho\sin(\phi)\) to get \(\displaystyle \iint_R f(x,y)dA = \iint_R f(\rho\cos(\phi), \rho\sin(\phi))dA\).

Recall that the area element \(dA\) in the original integral is thought of as the area of a rectangle: \(dA=dxdy\). Now that we’ve converted to polar coordinates, we need to adjust the area element.

In polar coordinates, we can partition the range of values of \(\rho\) into segments of equal length \(d\rho\); graphically, these are circles centred at the origin. We can also partition the values of \(\phi\) into small, equal angles \(d\phi\):

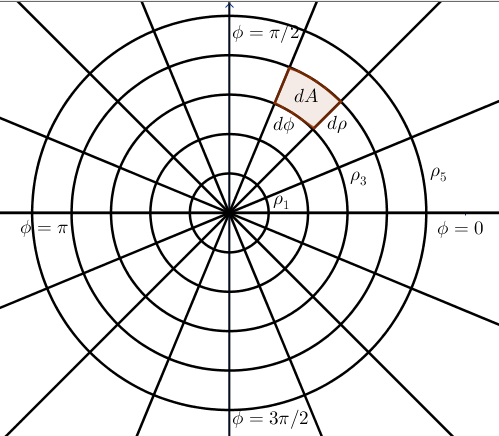
Figure 12.2: Partitioning of the polar plane

In order to find the area of \(dA\), recall that for a circle of radius \(r\), a sector of angle \(\theta\) has area \(\frac{r^2\theta}{2}\). Our sector is bounded above by \(\rho + d\rho\) and below by \(\rho\), so the area of the polar rectangle is the difference bewteen the area of the full sector of radius \(\rho + d\rho\) and the smaller sector of radius \(\rho\).

We get \[\begin{align*} dA &= \frac{1}{2}(\rho+d\rho)^2 d\phi- \frac{1}{2}\rho^2 d\phi\\ &= \rho~d\rho d\phi + \frac{1}{2} d\rho^2 d\phi \end{align*}\]

Since \(d\phi\) and \(d\rho\) are infinitesimally small, we can ignore the square term. We can now express our original integral using polar coordinates as follows: \[\displaystyle \iint_{R_{xy}} f(x,y)dA = \iint_{R_{\rho \phi}} f(\rho\cos(\phi), \rho\sin(\phi)) \rho~d\rho d\phi\]

It is extremely important to notice (and not to forget!) the factor of \(\rho\) in the integral expressed in polar coordinates! Also, notice that the domain \(R_{\rho\phi}\) indicates that we must write the domain in polar coordinates.

Exercise 12.2 Evaluate \(\displaystyle \iint_R (3yx^2+3y^3)dA\) where \(R\) is the semicircle of radius \(2\) that starts in the first quadrant and ends in the second quadrant.

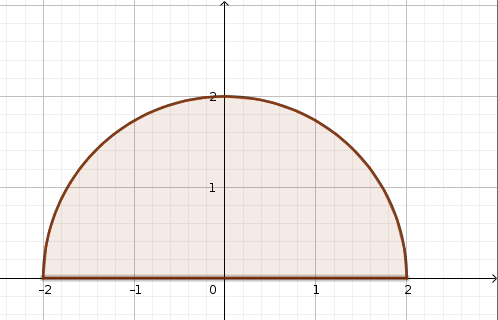
Figure 12.3: Semicircle of radius 2

Solution. To solve this problem, we can convert to polar coordinates by setting \(x=\rho\cos(\phi)\) and \(y=\rho\sin(\phi)\).

First, let’s describe the domain \(R\). We can describe the semicircle using the inequalities \[0\leq \rho\leq 2 \quad\mbox{and}\quad 0\leq \phi\leq \pi\]

Next, we convert the integrand to polar coordinates: \[3yx^2+3y^3 = 3y(x^2+y^2) = 3\sin(\phi)\rho^2\]

Now, we can set up and solve the integral, taking care to remember the factor of \(\rho\):

\[\begin{align*} \displaystyle \iint_R (3yx^2+3y^3)dA &= \int_{0}^{\pi}\int_0^2 3\sin(\phi)\rho^2~\rho~d\rho d\phi \\ &= \int_{0}^{\pi}\int_0^2 3\sin(\phi)\rho^3~d\rho d\phi \\ &= \int_0^{\pi}3\sin(\phi)\left (\frac{\rho^4}{4} \right|_{\rho=0}^2 d\phi\\ &= \int_0^{\pi}12\sin(\phi)d\phi\\ &= 24 \end{align*}\]

Exercise 12.3 Evaluate \(\displaystyle \iint_R x dA\) over the region bounded between the semicircle of radius \(1\) and the semicircle of radius \(2\) that start in the fourth quadrant and end in the first quadrant.

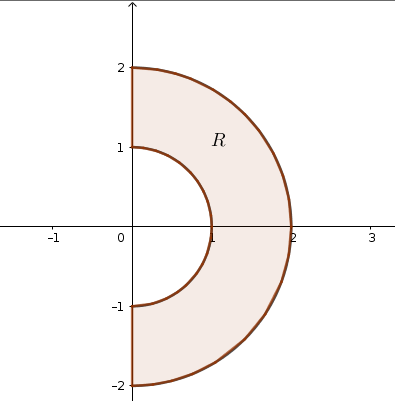
Figure 12.4: Domain of integration

Solution. First, let’s describe the domain \(R\). We can describe the region using the inequalities \[1\leq \rho\leq 2 \quad\mbox{and}\quad {- 3\pi/2}\leq \phi\leq \pi/2\]

Next, we convert the integrand to polar coordinates: \[x =\rho\cos(\phi)\]

Now, we can set up and solve the integral, taking care to remember the factor of \(\rho\):

\[\begin{align*} \displaystyle \iint_R x dA &= \int_{-3\pi/2}^{\pi/2}\int_1^2 \rho\cos(\phi)~\rho~d\rho d\phi \\ &= \int_{-3\pi/2}^{\pi/2}\int_1^2 \rho^2 \cos(\phi) d\rho d\phi\\ &= \int_{-3\pi/2}^{\pi/2}\cos(\phi) \int_1^2 \rho^2 d\rho d\phi \\ &= \int_{-3\pi/2}^{\pi/2}\cos(\phi) \left (\frac{\rho^3}{3}\right |_{\rho=1}^2\\ & = \int_{-3\pi/2}^{\pi/2} \frac{7}{3}\cos(\phi)\\ &= 0 \end{align*}\]